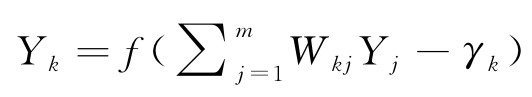基于BP神经网络的沥青路面沉陷发展预测
作者简介:
曹阳(1983-),男,本科,高级工程师,主要从事工程地质道路与桥梁施工的研究工作
路面沉陷是沥青路面的主要病害之一,沥青路面沉陷是指局部路面发生凹陷,一般由地基土质不良、路基或基层局部压实度不够、行车荷载等作用下产生竖向作用力等因素所致。沥青路面的沉陷会随着时间的推移不断增加,而使得路面剧烈变形,严重影响行车安全。
目前,道路工作者一般利用现场检测来获取沥青路面的沉陷数据,但高速公路公里数较长,如果单纯依靠现场仪器检测,会消耗大量的时间、人力、物力和财力。如果能根据有限的沉陷数据对整个沥青路面的沉陷发展进行预测,将能很大程度地解决耗时耗力的问题。HEINZ等[1]研究了一种基于二维激光扫描仪器的移动地图系统(MMS),使用沿高速公路的水平控制点以及重复通过的点云比较对MMS系统进行评估,利用数值波动将最小均方误差的椭球高度转换为控制点的物理高度系统,从而监测了道路的沉陷量。ZAHARI[2]基于先前观察到的沉降情况以及路面的整体情况,借助探地雷达的无损监测技术对沉降进行预测。何鎏[3]在雷达法的基础上进行改进,利用高密度地震映像技术对道路沉陷进行探测,有效真实地反映了道路沉陷情况,并判断了道路沉陷变形趋势。此类研究还有很多[4-5],其研究方法以及研究结果基本类似。然而,对于沥青路面沉陷这一内在因素错综复杂的变形来说,已有的研究大多数借助精密的科学仪器对沉陷纹理以及沉陷量进行提取,然后通过一系列计算对道路沉陷变形进行预测,计算方法较为复杂,且会消耗相当多的物力与财力。如果能够借助数学方法建立数据模型,对沉陷数据进行处理并预测道路的沉陷趋势,则可以有效解决当前的问题。
鉴于此,笔者以部分工程实测数据为研究基础,借助BP(back propagation)神经网络模型,对高速公路沥青路面的沉陷发展趋势进行分析、预测,并将预测结果与实测数据进行对比,验证了神经网络模型预测结果的合理性,为探究高速公路沥青路面沉陷病害的发展趋势提供一种新的研究方法。
1. BP神经网络概况
BP神经网络模型[6-7]是在人类对大脑神经网络认识理解的基础上人工构建的数学模型,其通过工程技术手段模拟构建出生物神经网络的结构特征与特点。与普通的拟合预测模型相比,BP神经网络能够仿照生物神经网络系统,对已知的数据样本进行学习、分析并掌握数据之间的复杂关系,通过大量数据的训练,使得模型不断完善,同时,可对完善后的数据模型进行记忆储存,最后对未知的新数据样本进行联想性预测。
BP神经网络的结构组成包含3部分,即输入层、隐含层(中间层)以及输出层,每层均有各自的神经元,每个神经元只有唯一的输出,而输入可以有多个,只要隐含层以及隐含层神经元个数足够多,则该模型可以反映出任意的非线性关系。BP神经网络的算法是全局逼近的学习算法,学习过程包含了信息的正向传播以及误差的反向传播。由输入层接受外部信息,通过神经元上的连接权值将信息传递给隐含层,由隐含层上多个互不联系的神经元对信息进行处理,最终通过输出层向外界输出处理结果。当输出结果的实际误差大于期望误差时,则进入反向传播过程,在该过程中不断进行迭代运算改变神经元连接权值,直至实现最终的收敛,达到可接受的目标误差,完成模型的建立。文章的研究目标为通过神经网络模型对影响路基沉陷的因素进行处理,进而对沉陷进行预测,而影响路基沉陷的因素与沉陷之间存在着复杂的非线性关系,因此利用BP神经网络模型模拟这种非线性映射关系并对其进行预测是较为恰当的。
2. 沥青路面沉陷发展的BP神经网络模型
2.1 神经网络模型输入与输出
BP神经网络在处理路面沉陷数据时有着独特的优越性,和其他处理方法相比,神经网络可以直接通过数据进行建模,处理拥有众多不确定因素、非线性关系的数据组,并且能够在学习反馈中剔除其他干扰因素,建立起反映数据之间真实关系的函数。
文章假定所要研究的沥青路面设计及施工符合规范要求,土层介质及厚度均匀(即各路段的压缩模量基本相同),采用层次分析与专家调查意见相结合的方法[8-10],选取4个主要影响因素(时间、交通量、填土高度、地基固结压缩程度[11-12])作为BP神经网络模型输入层的4个神经元,而输出层的神经元为沉陷量,是单一输出变量。
2.2 神经网络模型沉陷样本数据的选择
笔者选取某高速公路桩号K10+700断面数据作为研究对象。在试验路段施工前期,预埋了3个用钢筋混凝土浇筑成桩的观测基点,测点尺寸为15 cm×15 cm×150 cm(长×宽×高),结合全站仪、水准仪等土工观测仪器,测量出测点的沉陷;交通量由车辆动态称重检测系统获得;地基固结压缩程度由固结压缩试验测得。所有数据每半个月测量一次,共实测40组数据。
2.3 神经网络模型的迭代训练
利用MATLAB软件对模型进行训练迭代,训练过程由正向传播和反向传播两部分组成,在正向传播过程中,输入的沉陷影响指标从输入层经过隐层神经元的处理后,传向输出层,在输出层得不到期望的沉陷输出结果,则转入反向传播,此时沥青路面沉陷误差信号从输出层向输入层传播并沿途调整各层间连接权值和阈值,以使误差不断减小,直到其满足精度要求。在此过程中,隐含层向输出层传输的数据计算式为
| (1) |
输出层沉降指标的计算式为
| (2) |
式中:Xi为神经网络的输入,即影响沥青路面沉陷的4个影响指标;Yj为隐层单元第j个节点的输出;Yk为输出层第k个节点的实际输出,即路面沉陷指标;f(x)为激活函数;Wik,Wkj分别为输入层到隐含层和隐含层到输出层之间的连接权值;θj,γk分别为隐含层与输出层的阈值;l为输入层神经元节点数;m为隐含层神经元节点数。
2.4 神经网络预测模型的建立
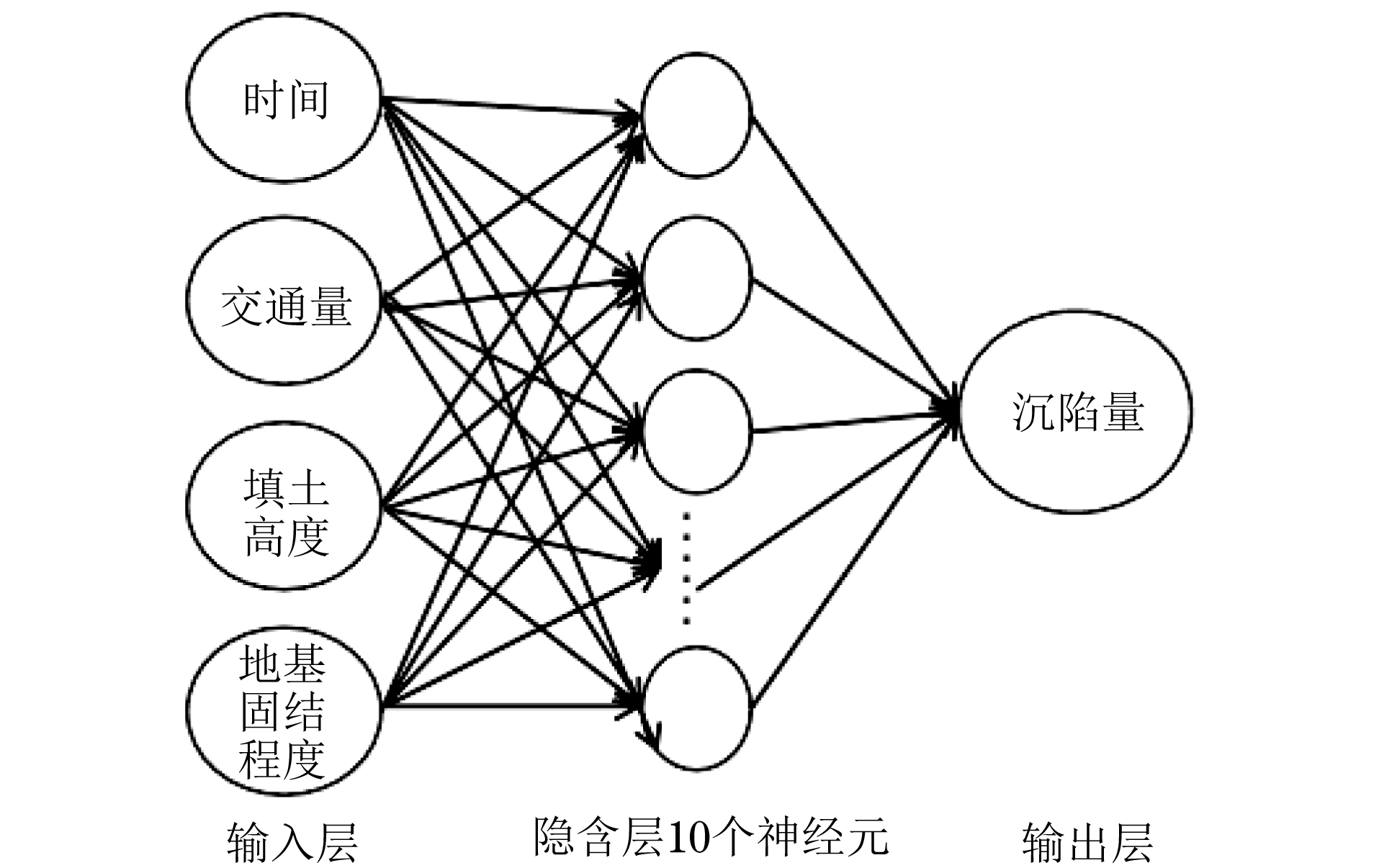
最终建立的沥青路面沉陷发展预测模型结构为4输入,1输出,隐含层为10个神经元的BP神经网络模型,其结构如图1所示。
2.5 模型运行结果精度分析
BP神经网络模型的准确性取决于是否有足够多且真实的训练样本数据,训练数据越多,预测越精确[13]。笔者的研究思路为充分利用2.2节中实测的40组数据,分别选用24组、28组、32组以及36组数据作为训练样本,依次得到4个BP神经网络预测模型(分别简称为模型Ⅰ、模型Ⅱ、模型Ⅲ及模型Ⅳ),并分别对37~40组的沉陷量进行预测。将4个模型预测的结果与实测结果进行误差比较,验证“训练数据越多,预测越精确”这一特点,同时选出最佳训练样本数,将由该样本数训练的预测模型的预测结果与其他预测方法的预测结果进行精度比较,验证BP神经网络模型在沥青路面沉陷预测方面的精确性。限于篇幅,文章以24组数据进行模型训练,对模型(记为模型Ⅰ)的运行结果精度进行详细分析。
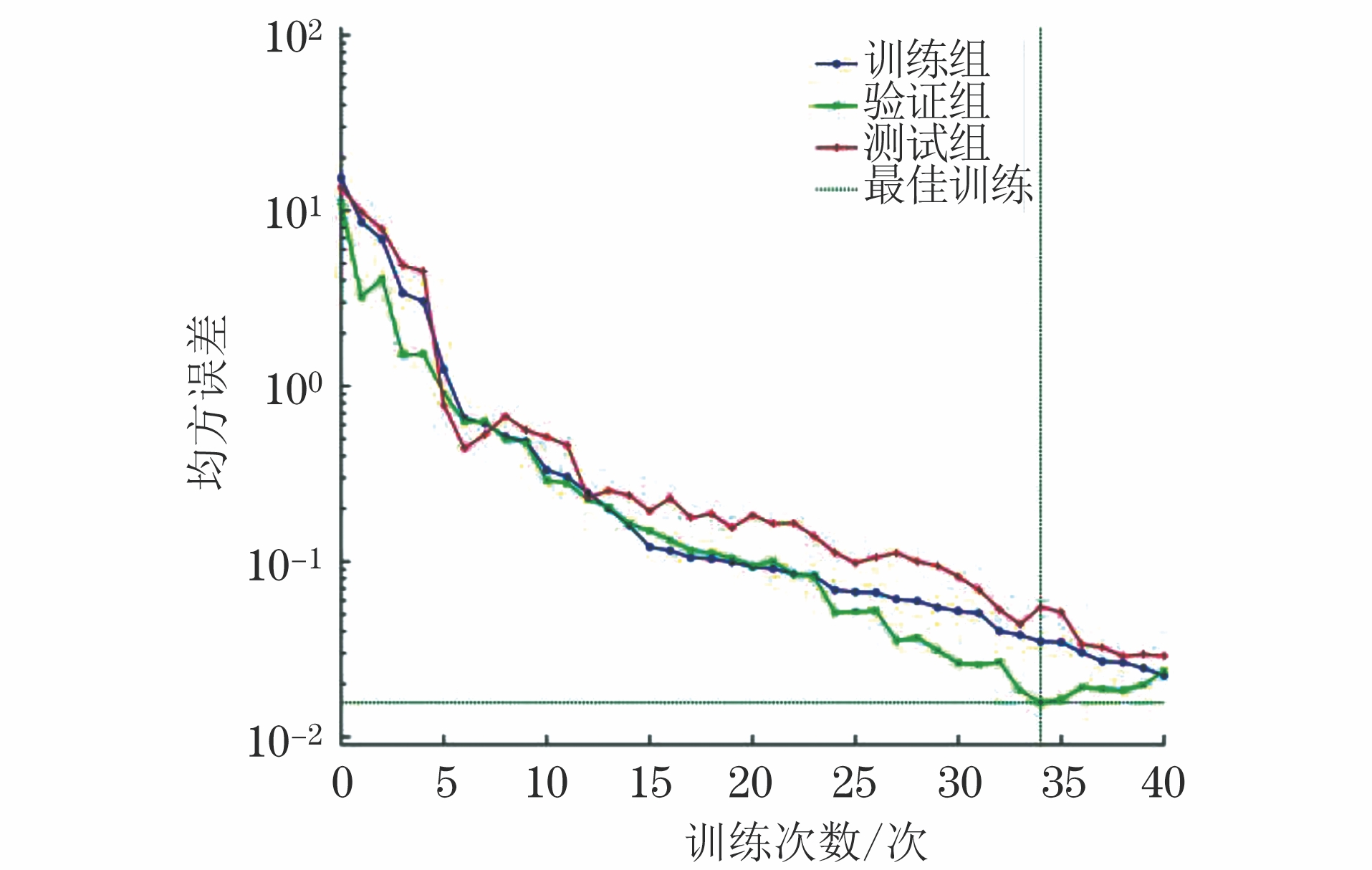
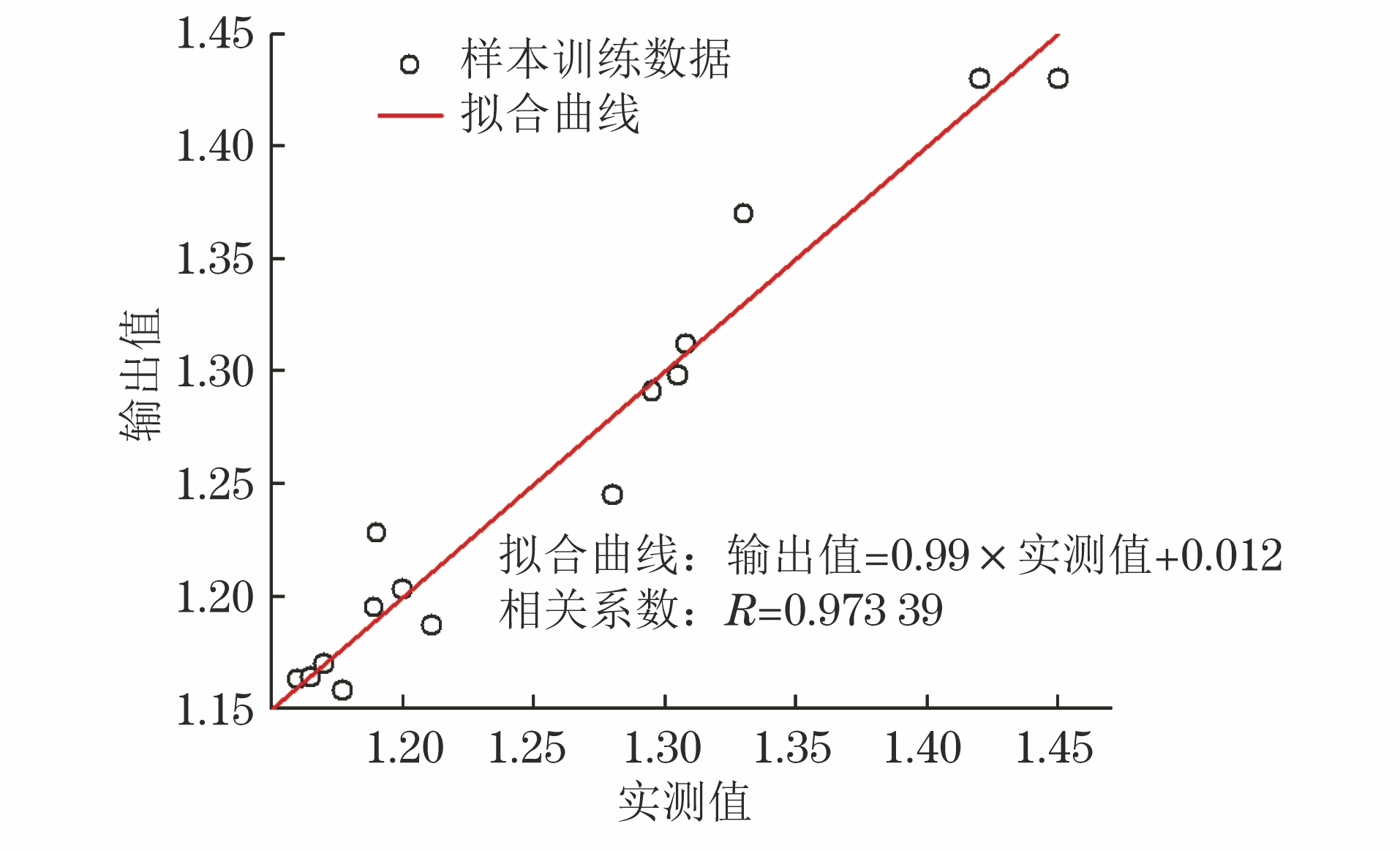
BP神经网络模型预测均方误差与训练次数关系曲线如图2所示,可见,预测模型验证组的均方误差随着训练次数的增加,呈现出先减小后增加的趋势,当训练达到34次时,均方误差最小(为0.012),表明此时模型的均方误差达到收敛,训练效果最佳。为验证训练模型的有效性与合理性,对拟合输出值与验证组的实测值进行回归分析,得到的拟合曲线如图3所示。
由图3分析可知拟合回归方程为:输出值=0.99×实测值+0.012。拟合回归所得的相关系数R为0.973 39,而相关系数R越接近1,则代表所建神经网络模型预测精度越高,可见,拟合所得的回归方程具有实际意义,表明训练之后的神经网络模型预测输出值与实测值之间有着显著的回归关系,所训练的模型能够有效对沥青路面沉陷进行预测。
进而分别利用28组、32组、36组数据,按照24组数据训练模型的过程对各自的神经网络模型进行训练,最终得到3个BP神经网络路面沉陷预测模型(记为模型Ⅱ,模型Ⅲ,模型Ⅳ),拟合所得的回归方程分别为:输出值=0.98×真实值+0.024;输出值=0.97×真实值+0.04;输出值=0.98×真实值+0.026。拟合所得的相关系数R分别为:0.987 55;0.987 88;0.987 92。由此可见,训练所得的3个预测模型预测精度较高,预测模型有效。
为寻找最佳样本数量,利用训练后的4个神经网络模型分别对K10+700断面处第37~40组数据进行沉陷预测,预测结果和实测值对比如表1所示。
| 神经网络模型 | 数据组 | 预测值/mm | 实测值/mm | 误差绝对值/mm | 误差/% |
|---|---|---|---|---|---|
| 模型Ⅰ | 37 | 1.083 | 1.054 | 0.029 | 2.75 |
| 38 | 1.153 | 1.068 | 0.085 | 7.96 | |
| 39 | 1.042 | 1.029 | 0.013 | 1.26 | |
| 40 | 1.011 | 1.041 | 0.030 | 2.88 | |
| 模型Ⅱ | 37 | 1.072 | 1.054 | 0.018 | 1.71 |
| 38 | 1.124 | 1.068 | 0.056 | 5.24 | |
| 39 | 1.045 | 1.029 | 0.016 | 1.55 | |
| 40 | 1.066 | 1.041 | 0.025 | 2.40 | |
| 模型Ⅲ | 37 | 1.044 | 1.054 | 0.010 | 0.95 |
| 38 | 1.101 | 1.068 | 0.033 | 3.00 | |
| 39 | 1.042 | 1.029 | 0.013 | 1.26 | |
| 40 | 1.032 | 1.041 | 0.009 | 0.87 | |
| 模型Ⅳ | 37 | 1.063 | 1.054 | 0.009 | 0.85 |
| 38 | 1.096 | 1.068 | 0.028 | 2.62 | |
| 39 | 1.020 | 1.029 | 0.009 | 0.87 | |
| 40 | 1.049 | 1.041 | 0.008 | 0.77 |
通过分析表1,得出以下结论。
(1)模型Ⅰ,模型Ⅱ,模型Ⅲ,模型Ⅳ的预测值和实测值的最大误差分别为7.96%,5.24%,3.00%及2.6%,表明训练组数据越多,预测模型的预测精度越高,训练后的模型对道路沉陷发展预测越精确。
(2)模型Ⅰ与模型Ⅱ的预测精度最大误差大于5%。如用此模型对道路沉陷进行预测,一定程度上会影响预测结果的精确性,导致沉陷判断不准确,错失沉陷治理的最佳时期;模型Ⅲ预测精度较模型Ⅰ与模型Ⅱ的有所提高,但该模型需要32组训练数据,收集原始数据的周期较模型Ⅱ增加了两个月;模型Ⅳ的预测精度最高,但其相较于模型Ⅲ,预测精度提高不大,同时,该模型的训练需要36组训练数据,收集数据的时间较模型Ⅲ又增加了两个月。因此,考虑到工程效率及预测精度,选取32组数据(模型Ⅲ)作为训练神经网络模型的最佳样本数。
3. 预测模型的适用性及误差比较
为进一步探究BP神经网络模型在沥青路面沉陷数据处理方面的优势以及沉陷预测的精度,采用二次曲线法[14]对同一组数据(37~40组)进行拟合分析并预测,对两种预测方法所得的结果进行分析比较,其中,BP神经网络模型选用预测模型Ⅲ,BP神经网络模型与二次曲线法预测误差对比结果如表2所示。
| 数据组 | 实测值/mm | BP神经网络模型 | 二次曲线法 | |
|---|---|---|---|---|
| 预测值/mm | 预测值/mm | 误差百分比/% | ||
| 37 | 1.054 | 1.044 | 1.095 | 3.89 |
| 38 | 1.068 | 1.101 | 0.988 | 7.49 |
| 39 | 1.029 | 1.042 | 1.124 | 9.25 |
| 40 | 1.041 | 1.032 | 1.098 | 5.48 |
分析表1,2可知,二次曲线法对沉陷数据的处理、预测有一定的效果,总体误差在10%之内,而BP神经网络模型的预测误差在4%以内,表明对于沥青路面沉陷的预测,BP神经网络模型拥有更高的预测精度。
4. 无损检测证书挂靠网结语
基于MATLAB软件,借助BP神经网络模型,对高速公路沥青路面的沉陷病害发展进行预测,得出以下结论。
(1)BP神经网络模型的沥青路面沉陷预测结果与实测数据误差较小,表明其应用于沥青路面沉陷发展预测具有可行性,BP神经网络模型的应用对研究沥青路面沉陷的发展规律及趋势具有重要的工程意义。
(2)相较于传统的二次曲线回归拟合法,基于大数据训练的BP神经网络具有更高的预测精度,且随着训练样本数据的增多,训练所得的模型预测精度提高。
(3)基于工程效率和预测精度的综合考虑,建议的训练样本数据为32组,此时预测误差在4%以内