基于贝叶斯优化的BiLSTM小管径弯管漏磁缺陷识别
作者简介:
作者简介:齐卜弘(2000—),女,硕士研究生,研究方向为特种设备健康监测及智能诊断
目前,小管径管道应用广泛,管道长时间服役后会出现腐蚀、老化等问题,进而引发管道运输事故,带来经济损失和环境污染[1]。小管径管道检测常采用漏磁检测技术,但小管径弯管处的磁导率分布不均匀,磁场强度相对于直管而言更难达到饱和,其产生的漏磁场分布复杂且易发生信号畸变。为了提高数据分析的准确率,减少不必要的工作量,有必要对数据进行优化处理[2]。
长短期记忆网络(Long short-term memory,LSTM)能弥补一般循环神经网络(Recurrent neural network,RNN)模型中的爆炸及消失等不足[3]。杜小磊等[4]将深层小波卷积自编码分析与LSTM相结合进行运用;赵志宏等[5]提出了一种基于BiLSTM(双向长短期记忆网络)的故障诊断方法;CABRERA等[6]将贝叶斯方法与LSTM模型相结合,提出了一种针对压缩机的故障检测方法。上述方法主要用于检测长输油气直管,而对小管径弯管漏磁缺陷识别的研究相对较少,因此,需要建立适用于弯管漏磁检测的缺陷识别模型。
文章建立了一种适应弯管漏磁场特点的贝叶斯优化BiLSTM识别模型,采用贝叶斯优化算法来确定BiLSTM的超参数调优,对BiLSTM网络的初始学习率和隐藏单元数进行优化。试验结果表明,该模型可对不同类型缺陷进行仿真模拟,提取漏磁信号特征量,提升了小管径弯管漏磁缺陷识别的精度和效率。
1. 小管径弯管漏磁信号缺陷识别方法
1.1 小管径弯管不饱和漏磁场及信号畸变
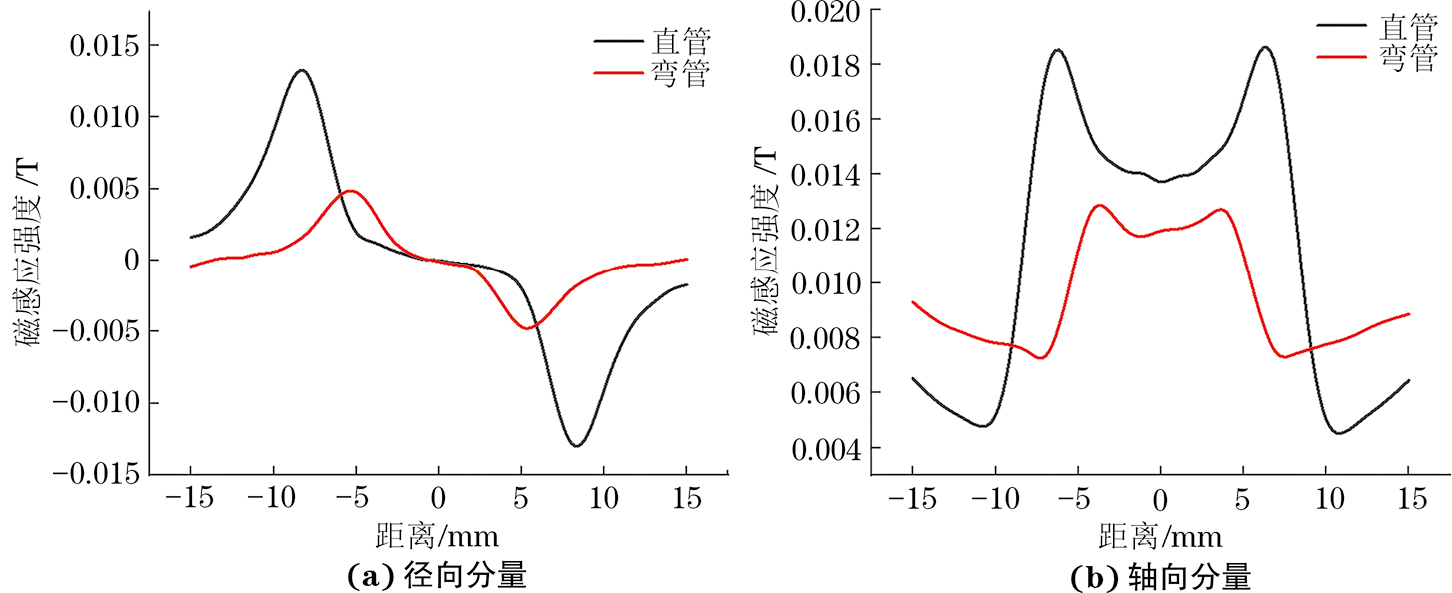
在进行漏磁检测时,提离值的大小直接决定了缺陷数据的可靠性[7]。检测直管时,提离值不发生相对变化,产生均匀饱和磁场;然而,弯管曲率的存在会导致检测处提离值发生变化,局部磁场可能因为磁路长度的增加或方向的改变而减弱,小管径管道的磁通量密度分布云图如图1所示。
分别提取直管和弯管处的磁感应强度,对比如图2所示。不饱和漏磁场使缺陷产生的额外磁通不能全部被闭合回路吸收,漏磁信号会发生不同程度的畸变且相对较弱,磁感应强度达不到最高值,信号特征可能变得模糊不清。
1.2 贝叶斯优化的BiLSTM
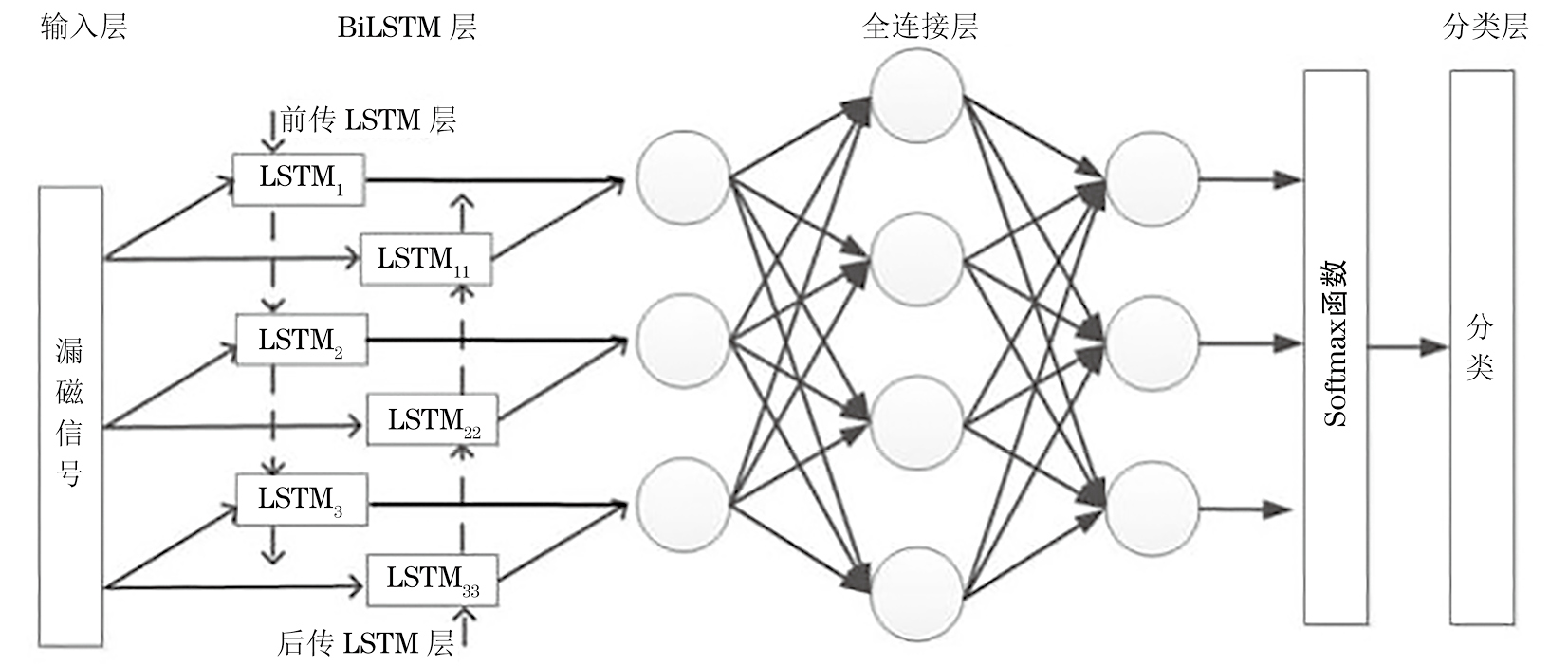
管道漏磁内检测生成的漏磁信号通常是时间序列数据,BiLSTM能够在序列的前后方向上捕获长期依赖关系。BiLSTM是对LSTM的改进,二者的输入是相同的,只是信息传递的方向不同,BiLSTM的结构示意如图3所示。
贝叶斯优化是一种有效的全局优化算法,其在优化的过程中,使用了贝叶斯定理,即

式中:f为未知目标函数;x1为已观测的集合;p(f)为f的先验概率分布;p(f|x1)为目标函数的后验概率分布。
2. 小管径弯管漏磁缺陷仿真分析
2.1 小管径弯管漏磁检测仿真模型
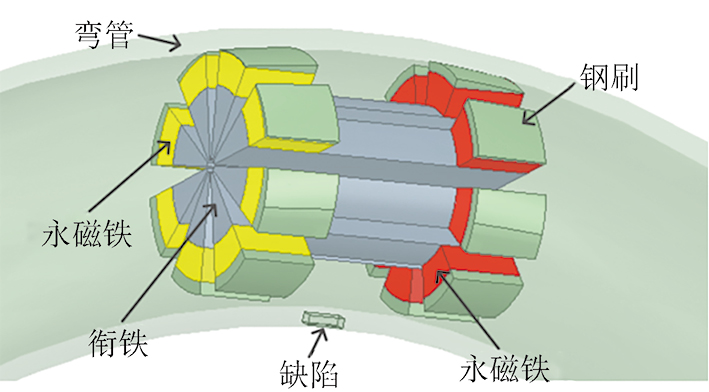
利用Maxwell仿真软件进行三维有限元仿真建模,其中,弯管尺寸为ϕ114 mm×8 mm(壁厚),材料为Q235钢,采用浮块式的磁化单元结构,永磁铁采用钕铁硼磁铁N48,衔铁和钢刷材料为DT4,其有限元模型如图4所示。
2.2 不同类型缺陷漏磁仿真信号
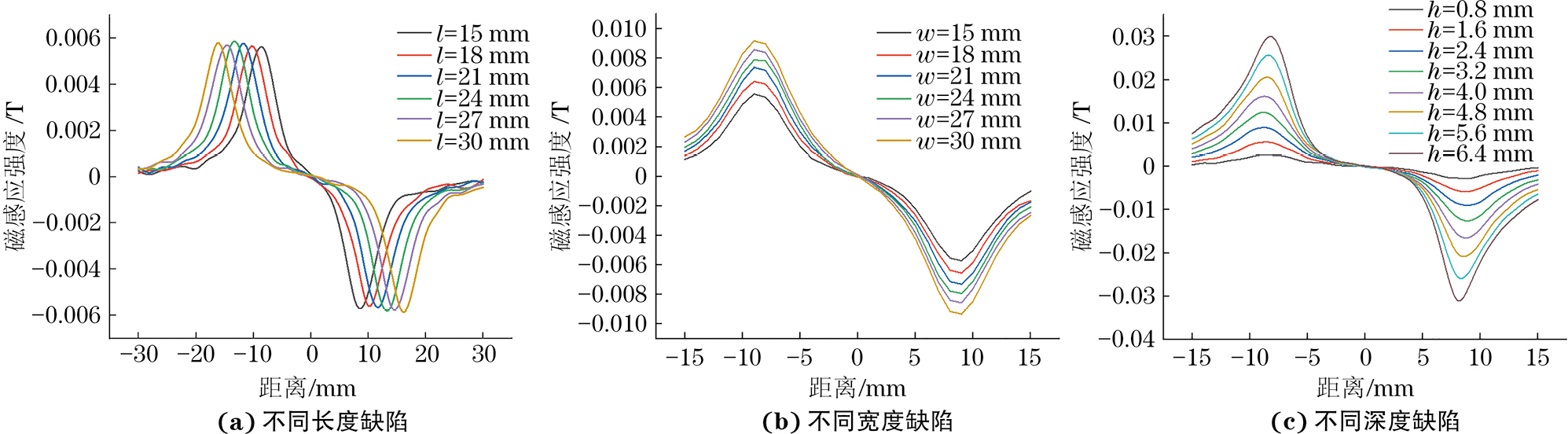
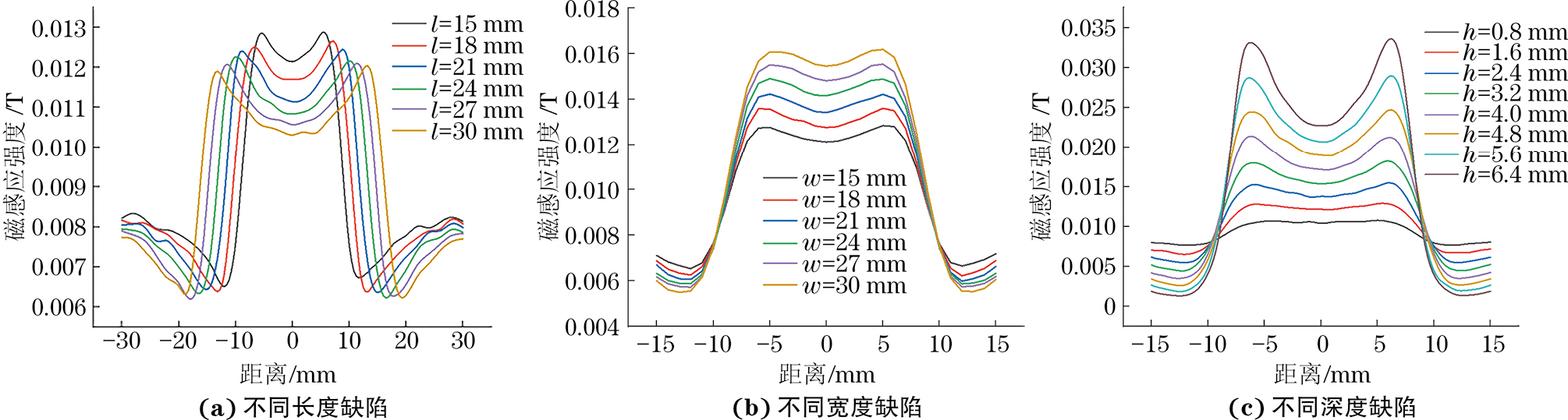
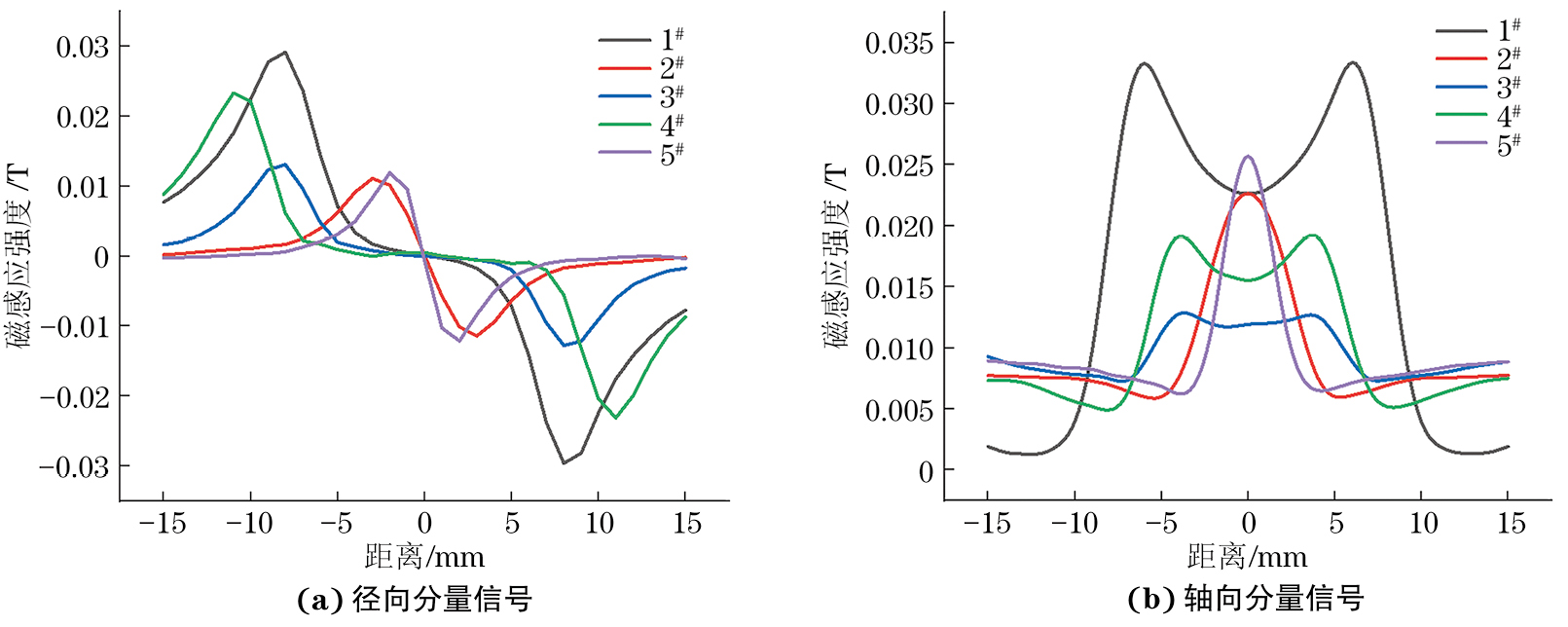
构建弯管漏磁不同类型缺陷数据集,缺陷类型为一般金属损失、坑状金属损失、轴向凹槽、轴向凹沟和周向凹槽,编号为1#~5#,每种缺陷的尺寸均匀变化并组合模拟,同时曲率半径分别取2D,3D,4D和5D(D为管道直径)。仿真缺陷数据集的具体参数如表1所示。以一般金属损失为例,不同尺寸的一般金属损失缺陷的漏磁仿真信号如图5,6所示。选取上述每组缺陷仿真信号中的一组进行分析,结果如图7所示。
| 缺陷 | 缺陷类别 | 曲率半径 | 长度l/mm | 宽度w/mm | 深度h/mm | 样本数量 |
|---|---|---|---|---|---|---|
| 1# | 一般金属损失 | 2D~5D | 15~30 | 15~30 | 10%~80%t(t为管壁厚度) | 140 |
| 2# | 坑状金属损失 | 5~10 | — | 140 | ||
| 3# | 轴向凹槽 | 10~30 | 2.5~5 | 200 | ||
| 4# | 轴向凹沟 | 10~30 | 1~5 | 200 | ||
| 5# | 周向凹槽 | 2~5 | 5~10 | 200 |
2.3 信号特征量的选择和提取
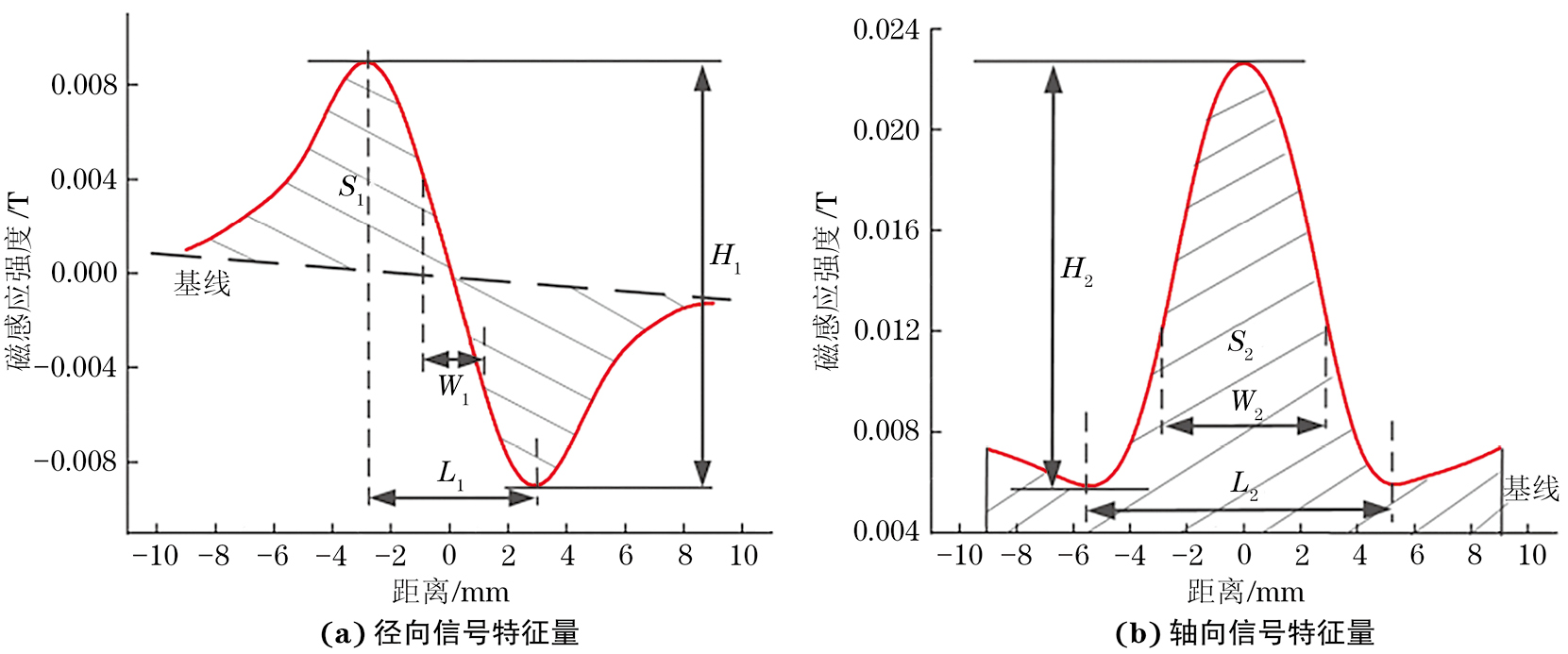
选择并提取了10个包含三轴漏磁信号的多模态特征值,包括漏磁信号波形的峰间距、峰峰值、半高宽、峰面积和波形能量等,其具体信息如表2所示。其波形曲线特征量定义示意如图8所示。波形能量是一定空间内漏磁信号波动部分的能量或信号的离散程度,其计算公式为

式中:a为所选波形起始点;b为波形结束点;f(x)为漏磁信号函数式。
| 信号特征名称 | 径向分量符号 | 轴向分量符号 |
|---|---|---|
| 峰峰值 | H1 | H2 |
| 峰间距 | L1 | L2 |
| 半高宽 | W1 | W2 |
| 峰面积 | S1 | S2 |
| 波形能量 | E1 | E2 |
3. 试验验证及分析
3.1 模型建立
根据上述方法提取数据集的特征量,得到模拟缺陷特征样本库,将所有样本按比率(训练集∶数据集为7∶3)进行分配,以此作为机器学习算法的输入,且每次训练输入样本的顺序随机。
将数据代入BiLSTM神经网络,隐藏层数初始设置为4,初始学习率预设为0.01,迭代次数设置为800,缺陷的编号作为输出进行训练和测试,得到缺陷识别结果的混淆矩阵如图9所示。
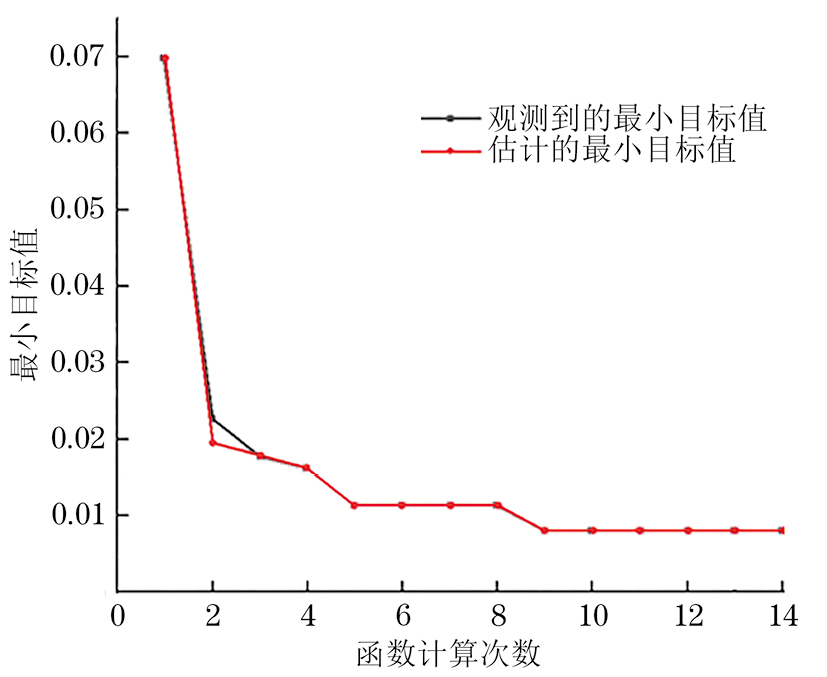
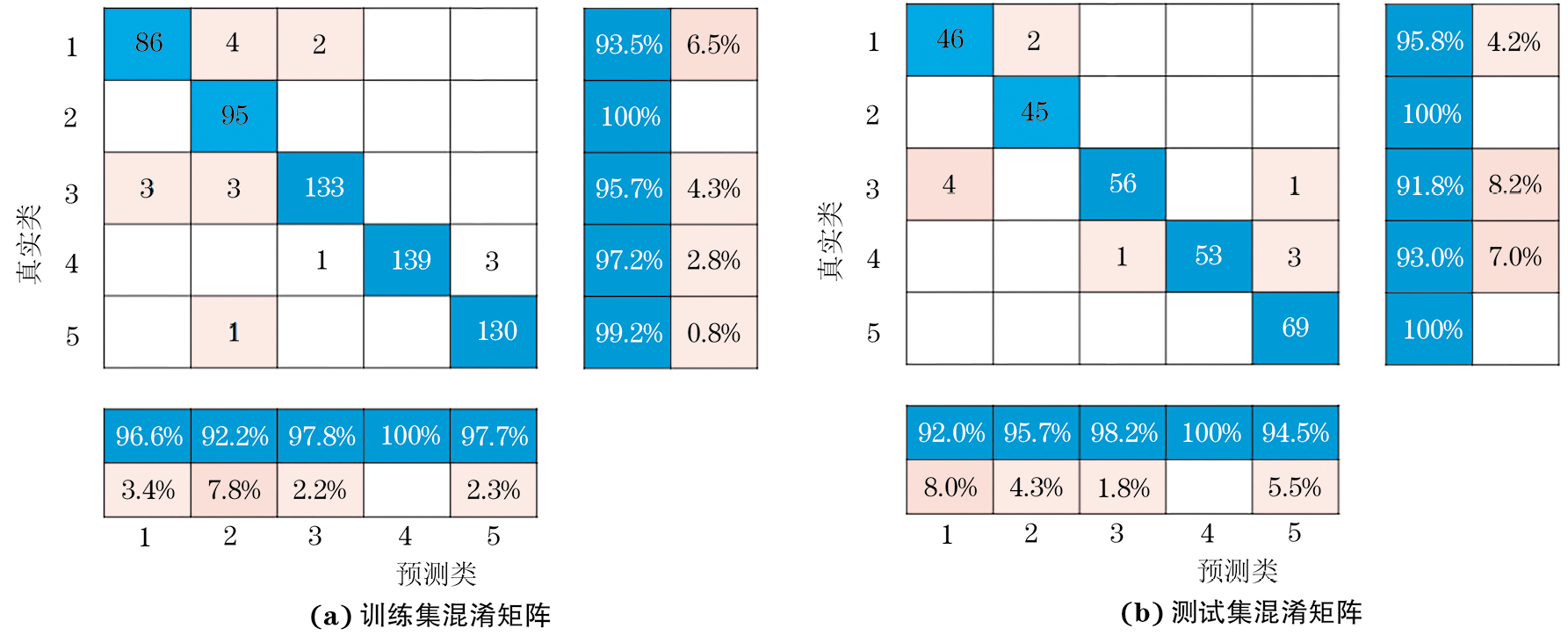
由于参数设置具有一定的盲目性,因此,使用贝叶斯优化对BiLSTM的初始学习率和隐藏层数进行优化,隐层数和初始学习率的优化范围分别为[10,20]和[10−3,10−2],迭代次数预设为14,贝叶斯优化迭代过程示意如图10所示,经过多次优化后模型性能达到最优,其缺陷识别结果的混淆矩阵如图11所示。
3.2 模拟测试及结果
BiLSTM优化前后的训练准确度和损失曲线对比如图12所示。当学习率为0.01时,BiLSTM在前50个迭代次数内的损失值下降很快,神经网络进入次优状态,最终损失值固定在0.4左右,并有波动;经过优化后的损失值曲线呈单调下降趋势,当迭代次数超过200次后,损失值为0,准确率明显提高。
为进一步验证贝叶斯优化的BiLSTM(BO-BiLSTM)网络的缺陷识别模型的优越性,将文章提出的优化网络算法分别与BP、LSTM神经网络进行对比,不同算法的识别结果准确率如表3所示,各种神经网络测试集的识别结果如图13所示,可见,BO-BiLSTM算法模型的检测性能均优于其他模型性能,其测试集的准确率达到96.07%,比优化前提高了2.13%。
| 参数 | 算法 | |||
|---|---|---|---|---|
| BP | LSTM | BiLSTM | BO-BiLSTM | |
| 准确率/% | 83.57 | 91.79 | 93.94 | 96.07 |
综上可知,BO-BiLSTM算法整体的识别率较高,运行速度更快,且具有广泛的学习能力和稳定性,更适合小管径弯管漏磁缺陷数据识别任务,对缺陷的识别拥有更高的置信度。
3.3 试验测试及结果
牵拉试验装置如图14所示,在试验过程中,将漏磁检测器缓慢且均匀地牵拉通过测试管道,当磁化单元经过管道时,在管道两侧产生与磁场强度成正比的电压差,霍尔传感器探头接收到漏磁场的变化,并在电子仓内对模拟信号进行A/D(模/数)转换,再将转换后的电信号传输至数据采集节。通过无缺陷管段时,初始电压值基本保持不变,经过预设缺陷管段时,缺陷周围的磁场强度发生改变,可在数据显示计算机上明显看出电压值的变化,然后通过对比分析多通道信号的波形强度和变化,选择信号幅值最大的通道,采用此通道的漏磁信号进行弯管缺陷识别分析。
试验管道的公称直径为114 mm,壁厚t为8 mm,曲率材料为Q235,对试验弯管人工预设1#~5#五种缺陷,每种缺陷设置两组,且每组缺陷深度均为10%t,20%t,30%t,40%t,50%t,60%t,70%t和80%t,弯管试件的缺陷信息如表4所示。
| 缺陷 | 尺寸 | 样本数量 | |
|---|---|---|---|
| 长度/mm | 宽度/mm | ||
| 1# | 15 | 15 | 16 |
| 20 | 20 | ||
| 2# | 5 | 5 | 16 |
| 10 | 10 | ||
| 3# | 10 | 5 | 16 |
| 20 | 5 | ||
| 4# | 10 | 2 | 16 |
| 20 | 2 | ||
| 5# | 5 | 10 | 16 |
| 5 | 20 | ||
两种算法的试验识别结果如表5所示,可知BO-BiLSTM算法对弯管缺陷的识别效果较好。由于仿真模拟的数据未包含噪声等干扰因素,因此其识别精度高于试验结果精度,但两者并不存在过大差距,表明该模型能较好地应用于小管径弯管漏磁缺陷识别。
| 算法 | 缺陷 | 检测内容 | ||
|---|---|---|---|---|
| 准确识别数量/个 | 误判数量/个 | 识别时间/s | ||
| BiLSTM | 1# | 14 | 2 | 15 |
| 2# | 12 | 4 | ||
| 3# | 15 | 1 | ||
| 4# | 13 | 3 | ||
| 5# | 12 | 4 | ||
| BO-BiLSTM | 1# | 16 | 0 | 10 |
| 2# | 15 | 1 | ||
| 3# | 14 | 2 | ||
| 4# | 14 | 2 | ||
| 5# | 15 | 1 | ||
4. 无损检测证书挂靠网结论
(1)漏磁检测时,弯管处是非均匀不饱和的漏磁场,可能产生畸变的漏磁信号,故需要建立适用于小管径弯管的缺陷识别模型。
(2)选取了漏磁信号的峰峰值、峰间距、峰面积、半高宽以及波形能量的多模态特征量,以此作为模型输入进行缺陷识别。
(3)建立的贝叶斯优化的BiLSTM模型缺陷识别方法,对一般金属损失、坑状金属损失、轴向凹槽、轴向凹沟和周向凹槽等5种缺陷的综合准确率达到96.07%,比改进前提高了2.13%;能满足小管径弯管漏磁缺陷识别的需求,并为缺陷量化提供了必要的数据基础和初步结论。
推荐阅读: