陶瓷基黏接件超声检测缺陷信号的处理方法
作者简介:
李爱华(1999—),女,硕士研究生,主要研究方向为无损检测、信号处理与重建
新型大厚度复合材料主要由陶瓷基复合材料和C/C复合材料黏接而成[1-3],这种复杂的制备工艺容易产生缺陷,因此需要对黏接件进行无损检测。超声检测技术是一种常用的检测方法[4],其根据超声回波信号的能量、波形及相位的改变对工件进行检测,而试件厚度过大会使回波信号的信噪比减小,因此,需要对回波信号进行降噪处理[5]。
小波阈值去噪算法是一种常用的去噪方法,该方法使用软、硬阈值函数对噪声分量进行滤除。软阈值函数存在恒定误差,容易丢失部分信号;硬阈值函数在阈值点处不连续,易导致去噪不彻底[9]。吴安全等[10]提出了一种半软阈值函数,但未解决软、硬阈值函数存在的问题。杜诗强等[11]引入了带指数参数的阈值估计器,解决了硬阈值函数不连续的问题,但仍存在恒定偏差。檀雪等[12]将指数函数引入到阈值函数中,改善了恒定误差,但仍存在信号有效信息丢失的问题。马杭等[13]引入双参数调节方式,使阈值函数调节变得更加灵活,但信号依然容易出现部分振荡的问题。综上所述,仅采用固定阈值函数对回波信号进行降噪,难以对缺陷信号进行有效提取。因此需对阈值函数进行改进,以达到良好的降噪效果。
基于上述研究,提出了一种改进的阈值函数降噪算法,在保留有效信息的前提下,改进了软硬阈值函数的恒定误差和不连续问题。仿真和试验结果表明,所提改进算法的去噪效果优于传统算法和其他几种改进算法的效果,且在实际中具有较好的应用效果。
1. 检测原理与信号处理原理
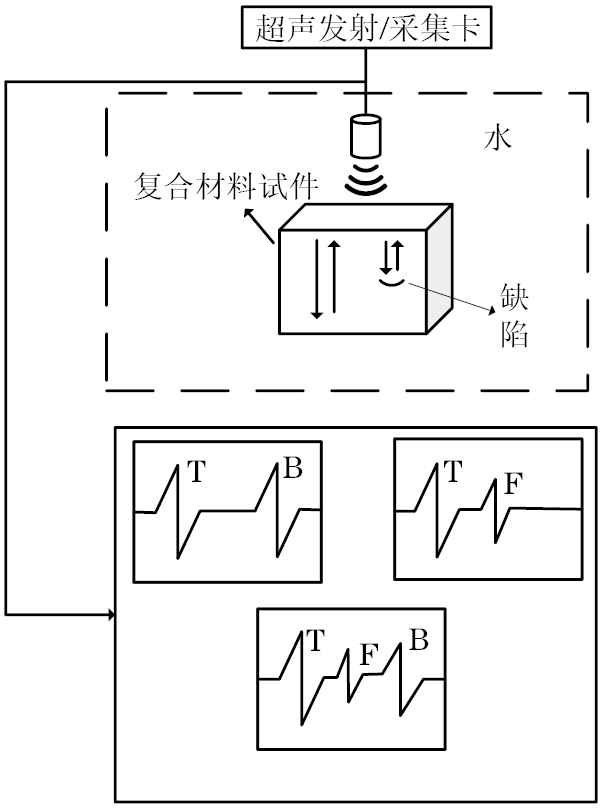
1.1 超声检测原理与材料
文章利用超声脉冲反射法来检测大厚度复合材料黏接试件的内部缺陷。脉冲反射法检测原理如图1所示,当超声波到达水/试件交界面时,表面会产生回波T,随后声波进入试件内部。如果检测路径上没有缺陷,超声波会继续传播并在试件底部产生底面回波B;如果路径上存在缺陷,当缺陷面积大于超声波的传播面积时,超声波会被缺陷全反射并被换能器接收,形成缺陷回波F。如果缺陷面积较小,超声波的一部分会被缺陷反射并被换能器接收,形成缺陷回波F,而剩余部分则继续传播并在试件底部反射形成底面回波B,该情况下的底面回波B的幅值通常小于无缺陷情况下的底面回波幅值。检测人员通过分析回波的特征,则可有效地识别和评估试件内部的缺陷情况。
因此,若信号中存在缺陷,即可通过超声纵波在复合材料中传播的速度v和缺陷距表面回波T的时间t来确定出缺陷距表面的距离x,关系式为
x=vt
式中:v为超声纵波在材料中的传播速度;t为超声波从缺陷位置传播到试件表面所需的时间。
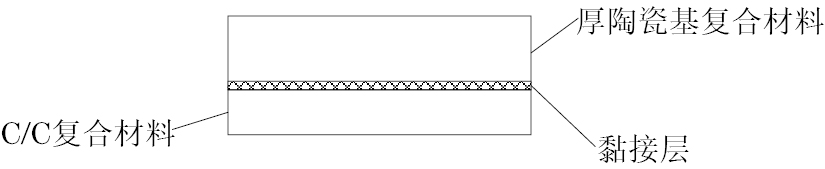
试验用的复合材料黏接试件结构如图2所示,主要由厚陶瓷基复合材料、黏接层和C/C复合材料3部分组成。由于试件的厚度较大,两种复合材料都属于多孔型复合材料,且以中、大孔为主,因此声波在传播过程中的散射和衰减会很大,换能器接收到的回波很小,容易被噪声掩盖,给缺陷特征提取和噪声识别带来一定困难,因此需要对接收到的信号进行降噪处理。
1.2 小波阈值去噪原理
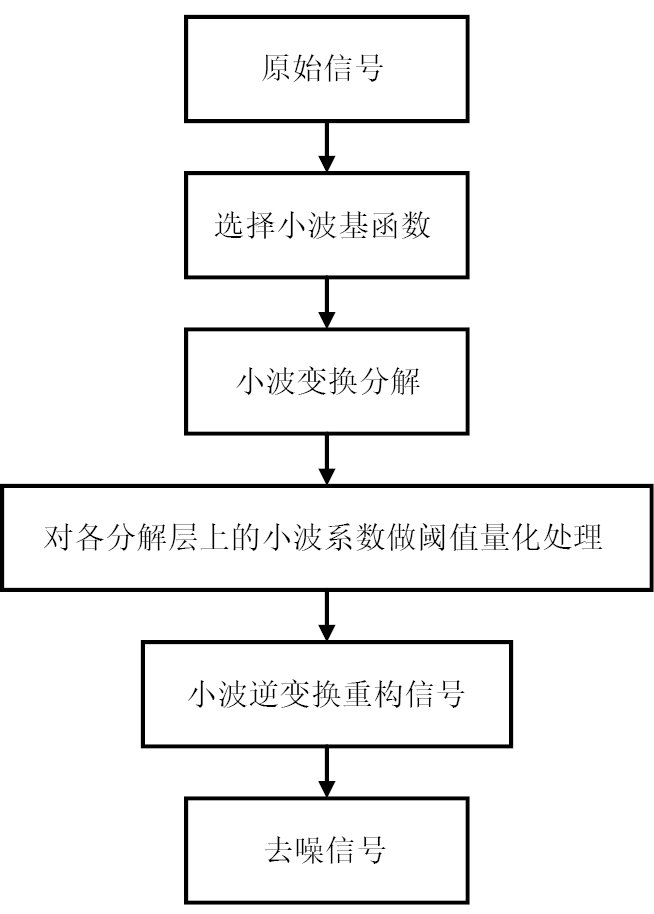
小波阈值去噪方法的基本原理是将噪声信号表示为原信号与服从高斯分布的噪声的叠加[14]。对需要降噪处理的信号进行小波变换后,可以分别获得原始信号和噪声的小波系数,这些系数代表了信号在不同频率范围内的特征,通常认为原始信号的小波系数较大,噪声信号的小波系数较小,因此,为了有效区分有用信号和噪声,需要选择一个合适的阈值作为判断标准[15]。小波阈值去噪的流程如图3所示,具体分为以下4部分。
(1)根据信号的特征,选择合适的小波基函数和尺度。
(2)使用选定的小波基函数和分解尺度对信号进行小波分解,得到不同尺度上的小波系数。
(3)对小波系数进行阈值处理。选择合适的阈值,将小于阈值的系数设为0(通常被认为是噪声信号),保留大于阈值的系数(通常被认为是有效信号)。常用的阈值处理方法为硬阈值和软阈值。
(4)使用处理后的小波系数进行小波逆变换,将处理后的系数重建为去噪后的信号。
1.3 改进的阈值处理方法
在对小波系数进行阈值处理时,传统方法有硬阈值处理和软阈值处理两种。
硬阈值函数可写为

软阈值函数可写为

式中:wj,k为小波分解系数;Wj,k为阈值处理后的小波系数;λ为阈值;sgn为符号函数。
为了解决软阈值函数存在恒定误差以及硬阈值函数不连续的问题,已有学者对阈值函数进行了多次改进和优化。孙万麟等[16]对软阈值函数进行了改进,然后对信号进行消噪处理,有效地保留了原始信号。刘冲等[17]研究了一种介于软硬阈值函数之间的阈值,并将该函数与VMD(变分模态)分解结合,对局部放电信号进行了降噪处理,较好地还原了原始信号。但两种改进函数的整体灵活性较差,不适用于复杂的噪声环境。
文章采用更加灵活的阈值函数,该阈值函数有两个调节参数,可通过调节这两个参数来应对复杂的噪声环境,即

式中:α,β为调节因子;e为自然对数的底。
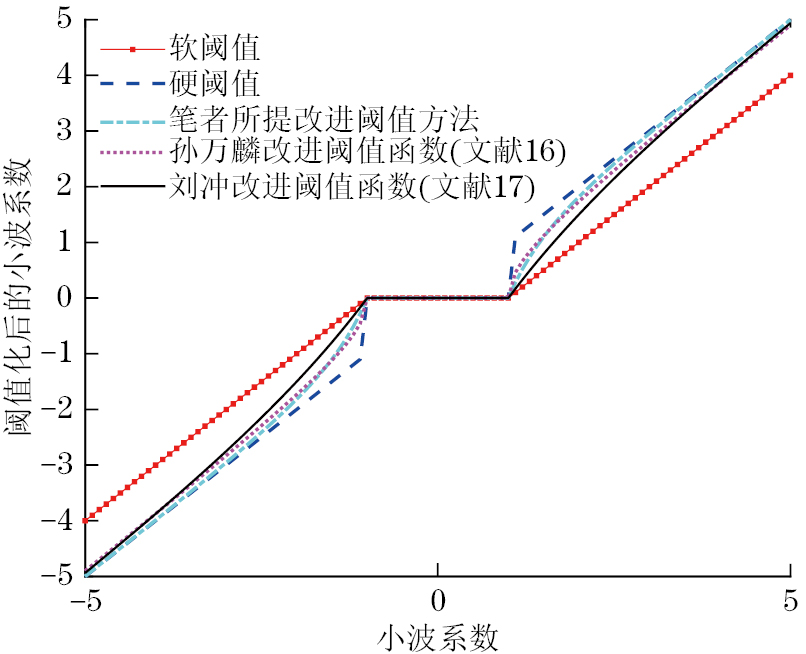
改进阈值函数曲线如图4所示,可见改进后的阈值函数在阈值点处是连续的,克服了硬阈值函数的不连续问题,并且该阈值函数可以通过调整α、β参数来使得其在超出阈值后迅速接近硬阈值函数,从而有效保留有用信号,解决了软阈值函数的恒定误差问题。与其他改进的阈值函数对比,所提方法更加连续、灵活,且平滑性更好。
2. 仿真试验
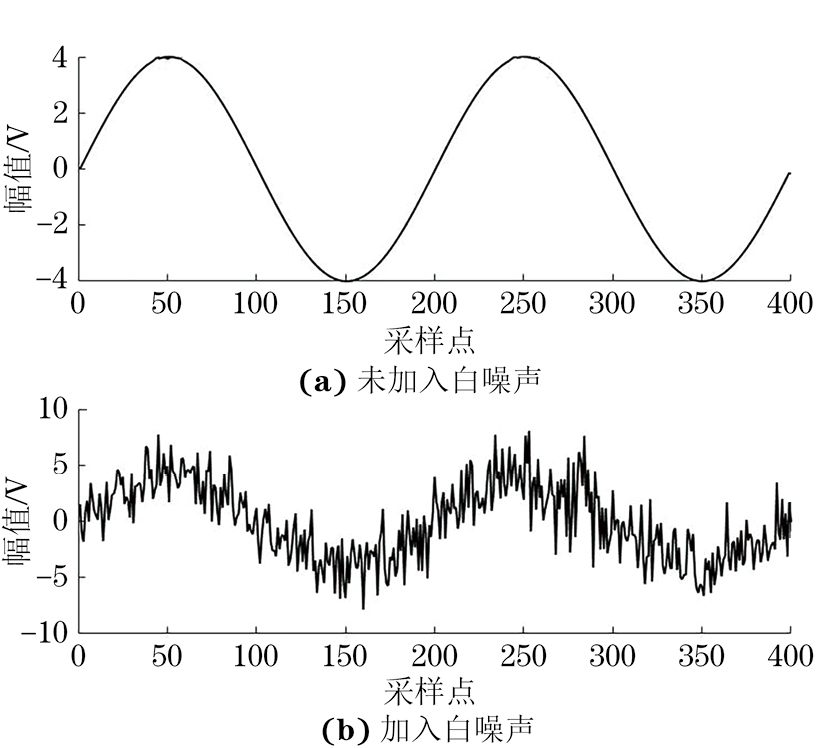
为了验证改进阈值函数去噪的可靠性,使用仿真软件对信号进行仿真。假设原始信号是一个幅值为4、频率为5的正弦波,将标准差为2的高斯白噪声添加到原始信号中,原始信号和被噪声污染的信号曲线如图5所示。
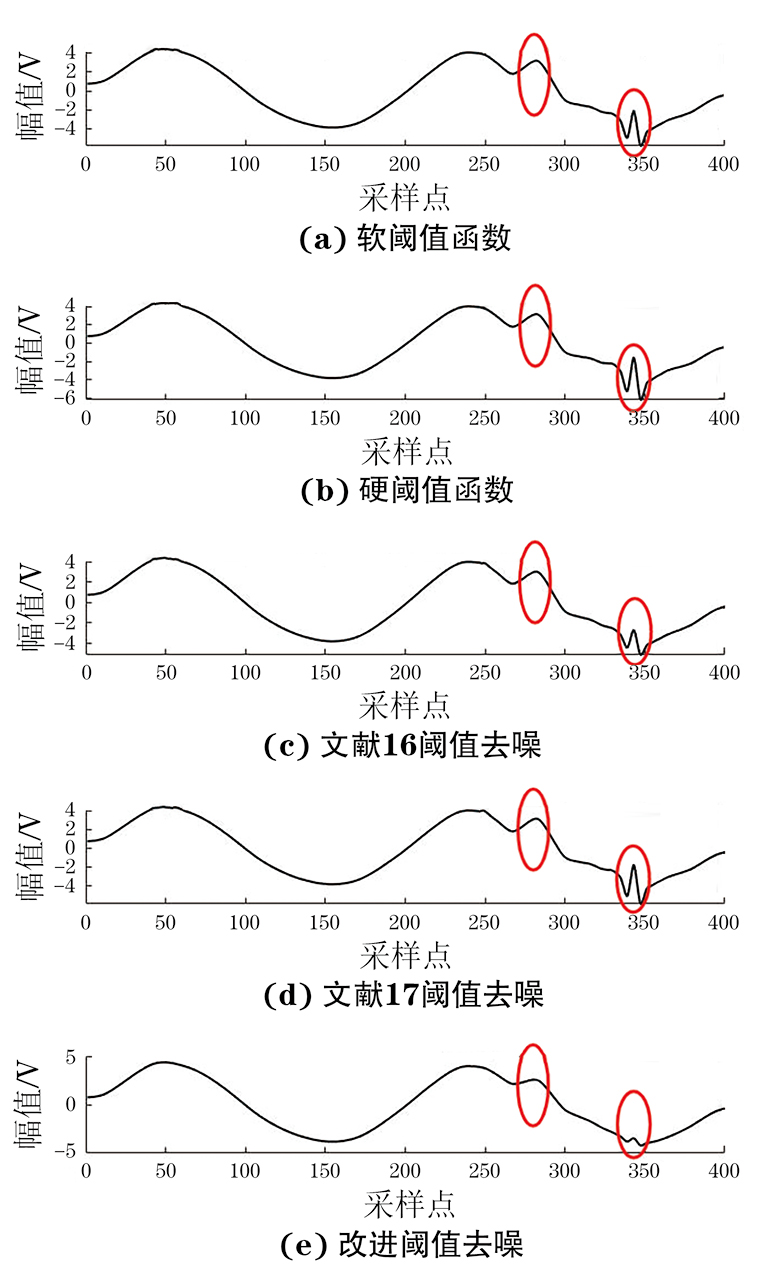
传统阈值函数和其他改进阈值函数去噪后的信号如图6所示,可以看出,去噪后信号在第282和第343个采样点处出现异常尖峰,但笔者所提改进阈值函数的异常尖峰比其他算法的小很多,去噪效果明显改善,去噪后的信号最接近原始信号。
3. 大厚度复合材料试件缺陷检测试验
采用频率为1 MHz的水浸聚焦探头,设置探头焦距为50 mm。对材料为Si/C陶瓷基复合材料和C/C复合材料的黏接件进行检测,其中试件外径为320 mm,厚度为60 mm,Si/C陶瓷基层厚度为40 mm,C/C层厚度为20 mm。在试件上设置3个孔洞缺陷,缺陷直径均为5 mm,每个缺陷距离外表面位置不同,分别为10 ,20 ,30 mm。大厚度复合材料试件结构如图7所示。
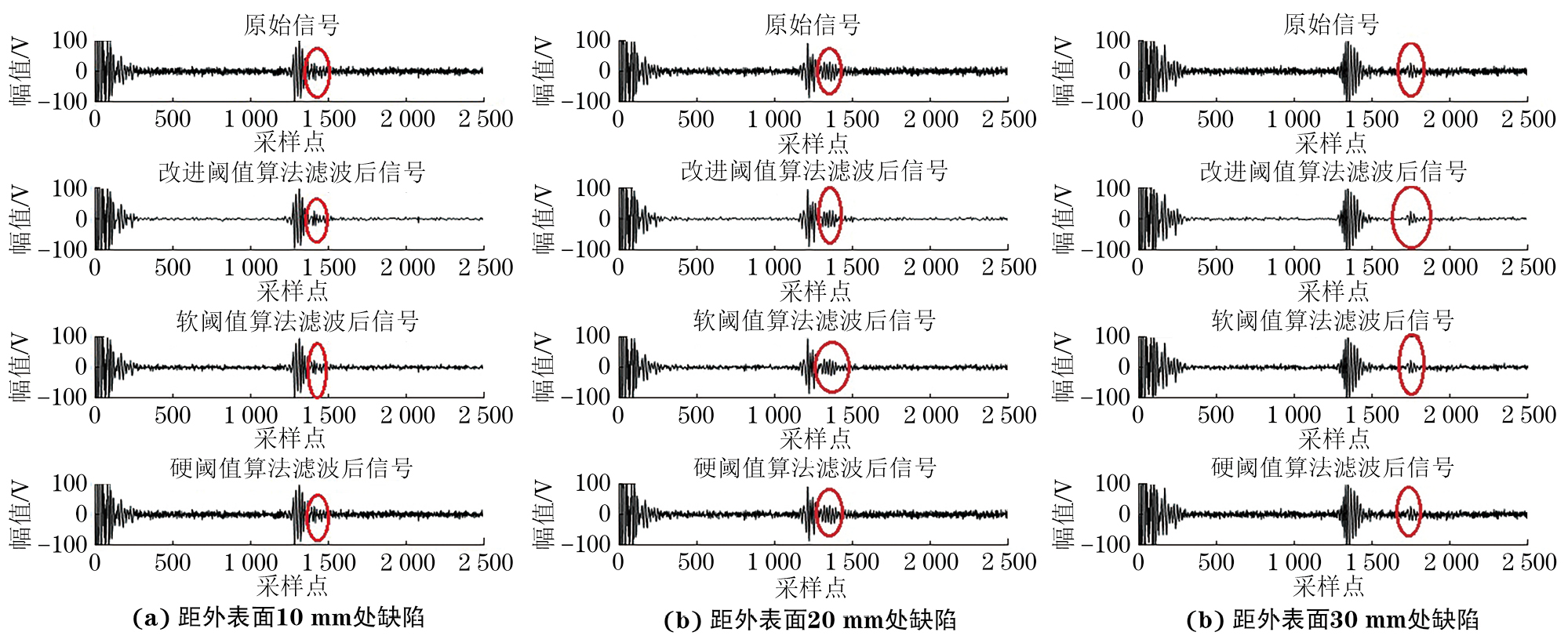
无缺陷和有缺陷时的超声回波信号对比如图8所示,探头在第1 234个采样点处接收到第一个回波,即表面波;在第1 751个采样点处接收到第二个回波,通过式(1)计算可知,该信号为距外表面30 mm处的缺陷信号,其几乎被噪声信号掩盖,缺陷特征信号易丢失。
使用Sym3小波基函数对原始信号进行3层小波分解,对分解后的信号进行阈值化处理并重构,得到的原始信号和降噪后信号曲线如图9所示,可见,红圈中的缺陷信号被噪声掩盖,而经传统软、硬阈值函数降噪后的信号噪声虽得到一定抑制,但去噪效果不够彻底,距表面10,20,30 mm处的缺陷信号仍不易与噪声信号分离,导致有效信号丢失;而经过改进阈值函数处理的信号,噪声得到明显抑制,去噪效果显著,缺陷信号幅值明显,有效信号得到保留。
文章采用信噪比(SNR)、均方根误差(RMSE)和噪声抑制比(NRR)3种噪声评价指标,对信号的去噪效果进行分析比较。表1~3为不同阈值函数方法得到的信噪比、均方根误差和噪声抑制比,从表中可以更加直观看到不同阈值函数的去噪效果。
| 去噪方法 | 深度 | ||
|---|---|---|---|
| 10 mm | 20 mm | 30 mm | |
| 改进阈值 | 13.460 0 | 12.880 8 | 14.201 6 |
| 软阈值 | 11.545 3 | 11.221 7 | 12.652 2 |
| 硬阈值 | 10.744 1 | 10.480 0 | 12.001 0 |
| 去噪方法 | 深度 | ||
|---|---|---|---|
| 10 mm | 20 mm | 30 mm | |
| 改进阈值 | 2.813 7 | 2.287 7 | 2.935 4 |
| 软阈值 | 3.507 6 | 3.482 5 | 3.508 6 |
| 硬阈值 | 5.433 4 | 5.357 7 | 5.341 8 |
| 去噪方法 | 深度 | ||
|---|---|---|---|
| 10 mm | 20 mm | 30 mm | |
| 改进阈值 | 11.519 8 | 14.386 2 | 12.580 3 |
| 软阈值 | 9.319 9 | 11.630 9 | 10.862 5 |
| 硬阈值 | 8.471 5 | 10.175 0 | 9.226 2 |
从表1~3中可以看出,使用改进阈值函数去噪信号的信噪比和噪声抑制比大于传统阈值函数结果,与软阈值函数去噪信号相比,信噪比提升了大约15%,噪声抑制比提升了大约20%;与硬阈值函数去噪信号相比,信噪比提升了大约21%,噪声抑制比提升了38%;改进阈值函数的均方根误差与软硬阈值函数结果相比是最小的。
最后根据改进阈值降噪处理后得出的特征信息进行C扫描重建,结果如图10所示,可以看出处理后的信号噪声得到了有效抑制,距表面10,20 mm的缺陷变得更加明显,距表面30 mm的缺陷边缘更加清晰,成像质量得到改善。
4. 结论
通过改进小波阈值函数,解决了软阈值函数的恒定偏差问题,以及硬阈值函数的不连续性问题,改进后的阈值函数通过改变α,β两个参数来调节阈值,提高了该函数在降噪中的灵活性,以尽可能地抑制噪声,并保留有效信号。与传统阈值函数对比,其信噪比大约提升了15%,噪声抑制比大约提升了20%,并且均方根误差小于软、硬阈值函数的。同时,使用该方法与传统阈值函数和其他改进阈值函数进行了对比试验,试验结果说明,改进算法的去噪效果优于传统阈值函数和其他改进阈值函数的效果,且能够有效地抑制大厚度复合材料缺陷检测中的噪声,保留缺陷信号的特征信息,具有实际应用可行性。
推荐阅读:2025年无损检测证书挂靠挂证价格